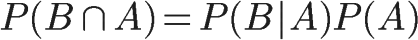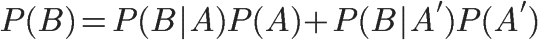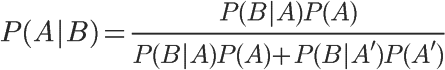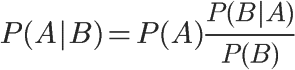1、自然语言处理简介
根据工业界的估计，仅有21% 的数据是以结构化的形式展现的[1]。在日常生活中，大量的数据是以文本、语音的方式产生（例如短信、微博、录音、聊天记录等等），这种方式是高度无结构化的。如何去对这些文本数据进行系统化分析、理解、以及做信息提取，就是自然语言处理（Natural Language Processing，NLP）需要做的事情。
在NLP中，常见的任务包括：自动摘要、机器翻译、命名体识别（NER）、关系提取、情感分析、语音识别、主题分割等。
在NLP与深度学习系列文章中，不会逐一解释各个NLP任务，而是主要介绍深度学习模型在NLP中的应用。整体分为以下几点：
首先介绍NLP基本流程以及在数据预处理方面的技术；而后会介绍最初期使用的神经网络：SimpleRNN、LSTM；继而引入使得文本处理性能得到很大提升的Attention机制以及Transformer模型；最后介绍近几年非常热门的预训练模型BERT，以及如何使用BERT预训练模型的例子
下面首先介绍的NLP任务的一个基本工作流程。
2、NLP 任务流程
典型的NLP任务分为以下几步：
数据收集
数据标注
文本标准化（Normalization）
文本向量化/特征化（Vectorization/Featuring）
建模前期主要是数据收集，并根据任务类型对数据做标注（例如情感分析中，对好、坏评价做标注）。接下来的2个步骤均是对文本进行预处理的步骤，为了提取文本中隐含的信息，最后通过机器学习建模，达到任务目标。其中 3 – 5 这几步是迭代的流程，为了模型的精度更准确，需要迭代这个过程，进行不断尝试。
数据收集以及标注并非在本文讨论范围内，接下来介绍文本标准化的目标与方法。
3、文本标准化
由于文本数据在可用的数据中是非常无结构的，它内部会包含很多不同类型的噪点。所以在对文本进行预处理之前，它暂时是不适合被用于做直接分析的。
文本预处理过程主要是对 文本数据进行清洗与标准化。这个过程会让我们的数据没有噪声，并可以对它直接做分析。
而文本标准化是NLP任务里的一个数据预处理过程。它的主要目标与常规数据预处理的目标一致：提升文本质量，使得文本数据更便于模型训练。
文本标准化主要包含4个步骤：
大小写标准化（Case Normalization）
分词（Tokenization）与 停止词移除（stop word removal）
词性（Parts-of-Speech，POS）标注（Tagging）
词干提取（Stemming）
3.1 大小写标准化
大小写标准化是将大写字符转为小写字符，一般在西语中会用到。但是对于中文，不需要做此操作。而且Case Normalization 也并非是在所有任务场景中都有用，例如在英文垃圾邮件分类中，一般一个明显的特征就是充斥着大写单词，所以在这种情况下，并不需要将单词转为小写。
3.2 分词
文本数据一般序列的形式存在，分词是为了将文本转为单词列表，这个过程称为分词（tokenization），转为的单词称为token。根据任务的类别，单词并非是分词的最小单位，最小单位为字符。在一个英语单词序列中，例如 ride a bike，单词分词的结果为 [ride, a, bkie]。字符分词的结果为[r, i, d, e, a, b, k, e]。
在中文中，分词的最小单元可以不是单个字，而是词语。
3.3 停止词移除
停止词移除是将文本中的标点、停顿词（例如 is，in，of等等）、特殊符号（如@、#等）移除。大部分情况下，此步骤能提升模型效果，但也并非在任何时候都有用。例如在骚扰邮件、垃圾邮件识别中，特殊字符相对较多，对于分辨是否是垃圾邮件有一定帮助。
3.4 词性标注
语言是有语法结构的，在大部分语言中，单词可以被大体分为动词、名词、形容词、副词等等。词性标注的目的就是就是为了一条语句中的单词标注它的词性。
3.5 词干提取
在部分语言中，例如英语，一个单词会有多种表示形式。例如play，它的不同形式有played，plays，playing等，都是play的变种。虽然他们的意思稍微有些区别，但是大部分情况下它们的意思是相近的。词干提取就是提取出词根（例如play 就是它各种不同形式的单词的词根），这样可以减少词库的大小，并且增加单词匹配的精度。
这些文本标准化的步骤，可以用于对文本进行预处理。在进一步基于这些文本数据进行分析时，我们需要将它转化为特征。根据使用用途不同，文本特征可以根据各种技术建立而成。如：句法分析（Syntactical Parsing），N元语法（N-grams），基于单词计数的特征，统计学特征，以及词向量（word embeddings）等。
其中词向量是当前主要的技术，下面主要介绍词向量。
4.文本向量化/特征化
向量化是将单词转为词向量的过程，也称为词嵌入（word embedding），这里嵌入的意思是说将单词所包含的信息嵌入到了向量中。
在word embedding出现之前，有2种文本向量化的方式，下面简单地介绍一下。
4.1基于单词计数的特征
此方法非常简单，首先将语料库文本进行分词，得到单词数。然后在对句子构建向量时，可以根据句子中包含的单词数构建向量。
举个例子，假设语料库为“我爱我的家，我的家是中国”。在进行分词后可以得到:
{'爱', '是', '，', '我', '中', '国', '家', '的'}
对于一个新的句子，例如”我爱我的国“，基于单词计数的表示即为：
[1, 0, 0, 2, 0, 1, 0, 1]
可以看到这种方法仅是对句子中的单词进行了统计，并不包含单词具体代表的含义（例如多义词的意义无法在此体现）。这种称为不包含上下文（context-free）的向量化。不过它提供了一种用于衡量两个文档相似度的方法。一般会通过余弦相似度或是距离来比较两个文档的相近程度。
4.2. 基于统计学的特征
在对文本做向量化时，一个常用的技术是词频-逆文档频率（Term Frequency – Inverse Document Frequency），常称为TF-IDF。TF-IDF 最初源于解决信息检索问题。它的目的是在于：基于单词在文档里出现的频率（不考虑严格的排序），将文档转化为向量模型。
这里Term Frequency很好理解，就是某个单词在文档中出现的频率。
在介绍Inverse Document Frequency（IDF）前，我们看一个例子。假设现在要通过单词检索文档，这里文档主要为各类食谱。如果我们使用单词如苹果、醋、酱油这类经常在食谱中出现的单词，则会有大量的文档可以匹配。而若是我们使用一些不常见的词，例如黑莓，则可以显著缩小要搜索的食谱文档。也就是说，若是一个单词越是不常见，则越有助于检索需要的文档。所以对于这类不常见的词，我们希望给它一个更高的分数。反之，对于在各个文档中都频繁出现的词，希望给它们更低的分数。这就是IDF的思想。
TF-IDF 的计算，数学上表示可以写为：
TF-IDF = TF(t, d) x IDF(t)
这里t表示term，也就是单词；D表示Document，文档。
IDF的定义为：
IDF(t) = log( N/(1+nt) )
这里N表示语料库中的文档总数，nt表示有多少文档中存在单词t。这个加1是为了防止除以0。
4.3 词向量
上面介绍了2种方式，仅仅是解决了用一个向量代表了一个文档，但无法体现词与词之间的关系。而从常理来看，词与词之间是存在联系的。例如，炒锅与锅铲，这2个词，从直觉上来看，会经常在一起出现。而炒锅与人行横道，应该基本不会出现在一起。
词向量，也称为词嵌入，是将单词映射（或称嵌入）到一个高维空间中，使得意义相近的词在空间内距离相近；意义不同的词在空间内距离相远。
4.3.1Word2Vec
在词嵌入技术中，一个具有时代意义的方法是Word2Vec，于2013年由Google的工程师提出。它本身算是神经网络处理任务的一个副产品。例如，搭建一个神经网络，每次取一个批次的5个单词，中间的单词作为target，周围的4个词作为输入，来训练神经网络。初始的输入词向量使用one-hot编码。这样再训练完成后，第一层的输入层参数，即为所得的词向量矩阵。
Word2Vec论文提出了2种训练方式：continuous bag-of-word（CBOW）和continuous skip-gram。在论文提出时，CBOW是当时主流方法；不过最后skip-gram模型与负采样的集成方法，已经成了Word2Vec的代名词。
Word2Vec已经有很多优秀的文章讲解过，在此不再赘述。下面主要举例说明skip-gram负采样的方式。
假设语料库中有一条句子为：“需要把鱼煎到棕黄再翻面”。
我们设置一个单词数为5的窗口，也就是一次处理5个单词，例如“要把鱼煎到”这5个词。中间的词“鱼”会被用于输入到搭建好的神经网络中，用于预测它前面的2个词（“要把”），以及后面的2个词（“煎到”）。
假设语料库中有10000个单词，神经网络的任务就是要判断给定一组词，它们是否相关。例如，对（鱼，煎）判断为true，对（鱼，树）判定为false。这种方法就是Skip-Gram Negative Sampling（SGNS），基于的假设就是：与某个词相关的词会更高概率一起出现（或是离的不远），所以可以从一段短语中拿出一个词，用于预测它周围的词。
SGNS的方法可以显著降低训练超大型语料库的时间，最终第一层输入层的权重矩阵即为词向量矩阵。
当然，Word2Vec也有它的局限性，一个典型的局限就是没有全局的统计信息，因为它在训练的时候最长是以一个窗口为单位，能看到的只有窗口内的上下文信息。
4.3.2 GloVe
GloVe (Global Vectors for Word Representation) 模型于2014年提出，于Word2Vec论文发表1年后。它们生成词向量的方法非常相似，都是通过一个词（例如上述例子中的“鱼”）周围的词，来生成这个词（例如“鱼”）的词嵌入。不过相对于Word2Vec，GloVe利用了全局的文本统计信息，也就是构建语料库的共现矩阵。 共现矩阵简单来说，就是2个单词在窗口中一同出现的次数，以矩阵的形式表示。在有了全局统计信息（共现矩阵）后，接下来的问题是如何将全局信息应用到词向量生成中。
在原论文中，作者用了2个单词ice和steam来描述这个理念。假设有另一单词solid，用来探查ice与steam之间的关系。在steam上下文中出现solid的概率为 p(solid | steam)，从直觉上来看，它的概率应该会很小（因为steam与solid从直觉上同时出现的概率不会很高）。
而对于ice上下文中出现solid的概率 p(solid | ice)，直觉上应该会很高（因为ice是固体，直觉上它们同时出现的概率会很高）。
那如果我们计算p(solid | ice)/ p(solid | steam) 的比值，则预期的结果应该会很高。
而若是用gas作为探测词，则 p(gas | ice)/p(gas | steam) 的比值应该会很低（因为gas是气体，在直觉上在steam的上下文中出现的概率高，而在ice的上下文中出现的概率低）。
而若是用water这类与ice和steam相关性都很低的词作为探测词，则p(water | ice)/p(water | steam) 的概率应该接近于1。论文中也举了另一个与ice和steam不相干关的词fasion，p(fasion | ice)/p(fasion | steam) 的结果也近似于1。
也就是说，共现矩阵的概率的比值，可以用来区分词。GloVe的过程就是确保这种关系被用于生成词嵌入，将全局信息引入到了词向量的生成过程中。
若是对GloVe方法有兴趣，可以阅读这位博主的介绍：
https://blog.csdn.net/XB_please/article/details/103602964
或是GloVe论文：
https://nlp.stanford.edu/pubs/glove.pdf
对于GloVe的效果，论文中提到是远高于word2vec。
在使用GloVe时，可以直接从stanford的官网下载预训练的GloVe词嵌入，分为50、100、200、300维的词嵌入。地址为：
http://nlp.stanford.edu/data/glove.6B.zip
4.3.3 BERT
Word2vec与GloVe都有一个特点，就是它们是上下文无关（context-free）的词嵌入。所以它们没有解决：一个单词在不同上下文中代表不同的含义的问题。例如，对于单词bank，它在不同的上下文中，有银行、河畔这种差别非常大的含义。BERT的出现，解决了此问题，并极大地提升了baseline。
另一方面，BERT还解决了GloVe的一个局限性问题，就是：词库不够。例如在使用GloVe预训练的词嵌入应用到 IMDB数据集上时，大约有15%的词不在GloVe的词库中。当然，这也是由于一个词会有多种形式，导致所需词库巨大。
在BERT中，使用了WordPiece的分词方法，词库大小为30000。其实这个大小是远小于GloVe的词库大小，GloVe词库为40000。这是由于BERT使用的subword分词方法可以显著减少词库的大小，WordPiece基于的是BPE（Byte Pair Encoding），BPE属于subword分词法中的一种。
简单地说，subword分词法主要做的就是将单词进行进一步的拆分，让词库更加精简。更精简的词库可以降低训练时间，并减少内存使用。Subword分词法，以英语语言为例，举个简单的例子，例如在词库中引入2个新的词，分别为-ing与-ion。则任何结尾为-ing或-ion的词，均可分为2个词，一个是前缀词，一个是-ing或-ion中的任何一个。这样就极大减少了词库的大小。当然，WordPiece以及BPE中使用的方法并没有这么简单。若是对BPE与WordPiece算法有兴趣，可以阅读这位博主的介绍：
https://www.cnblogs.com/huangyc/p/10223075.html
在BERT中，对它使用的WordPiece分词，我们可以看一个例子：
#!pip install transformers==3.0.2
import tensorflow as tf
from transformers import BertTokenizer
import numpy as np
bert_name = 'bert-base-cased'
tokenizer = BertTokenizer.from_pretrained(bert_name, add_special_tokens=True, do_lower_case=False, max_length=150, pad_to_max_length=True)
# tokenize single sequence
tokens = tokenizer.encode_plus("Don't be lured",
add_special_tokens=True,
max_length=9,
pad_to_max_length=True,
truncation='longest_first',
return_token_type_ids=True)
res = []
reverse_dic = [(id, item) for item, id in tokenizer.vocab.items()]
for tk in tokens['input_ids']:
res.append(reverse_dic[tk][1])
print(res)
['[CLS]', 'Don', "'", 't', 'be', 'lure', '##d', '[SEP]', '[PAD]']可以看到其中lured被拆分成‘lure’与‘##d’。另外的[CLS] 、[SEP] 与[PAD] 是BERT Tokenizer中的保留词，分别代表“分类任务”、“Sequences之间的间隔”，以及序列补全（序列补全与截断是NLP任务中常用的方法，用于将不同长度的文本统一长度）。
更多有关BERT的具体内容会在后续BERT章节进行介绍。
5、总结
在文本数据进行了标准化与向量化后，即可根据任务类型进行建模，将数据输入到模型中进行训练。文本标准化 => 向量化 => 建模，也是一个迭代的过程。下一章会介绍NLP任务早期建模使用的神经网络：SimpleRNN、LSTM以及双向循环神经网络。
References
[1] Natural Language Processing | NLP in Python | NLP Libraries (analyticsvidhya.com)
[2] Essentials of NLP | Advanced Natural Language Processing with TensorFlow 2 (oreilly.com)
[3] Word2Vec与Glove：词嵌入方法的动机和直觉
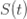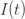来表示；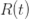
来表示；
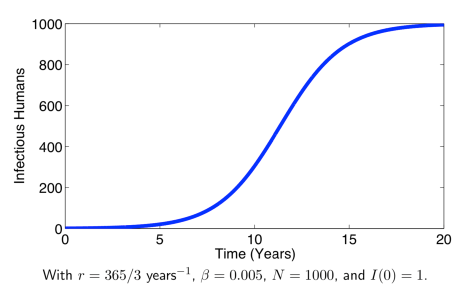
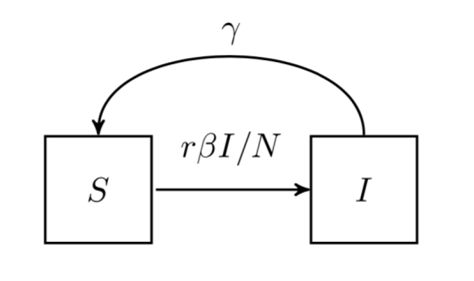
来表示；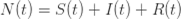
。如果暂时不考虑人口增加和死亡的情况，那么N(t)是一个恒定的常数值。
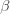：表示感染者接触到易感者之后，易感者得病的概率；
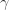：表示感染者康复的概率，有可能变成易感者（可再感染），也有可能变成康复者（不再感染）。
，
。
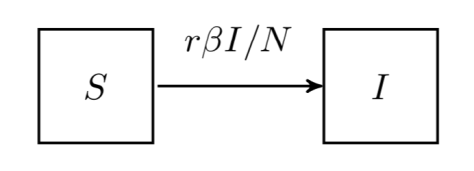
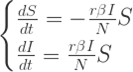
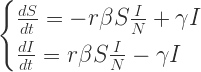
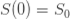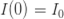