关于传染病的数学模型，在许多年前数学界早已做过研究，根据传染病的传播速度不同，空间范围各异，传播途径多样，动力学机理等各种因素，对传染病模型按照传染病的类型划分为 SI，SIR，SIRS，SEIR 模型。如果是按照连续时间来划分，那么这些模型基本上可以划分为常微分方程（Ordinary Differential Equation），偏微分方程（Partial Differential Equation）等多种方程模型；如果是基于离散的时间来划分，那么就是所谓的差分方程（Difference Equation）。差分模型其实是微分模型的离散形式，所以我们只讨论微风方程模型。
首先要介绍一些常用的符号：在时间戳 上，可以定义以下几种人群：
•易感者（susceptible）：用符号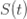
来表示；
•感染者（infective）：用符号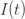
来表示；
•康复者（Recoverd）：用符号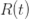
来表示；
其次，在时间戳t上，总人口是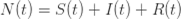
。如果暂时不考虑人口增加和死亡的情况，那么N(t)是一个恒定的常数值。
除此之外，
•r表示在单位时间内感染者接触到的易感者人数；
•传染率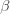
：表示感染者接触到易感者之后，易感者得病的概率；
•康复率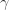
：表示感染者康复的概率，有可能变成易感者（可再感染），也有可能变成康复者（不再感染）。
在进行下面的分析之前，先讲一个常微分方程的解。
一、SI 模型（Susceptible-Infective Model）
在 SI 模型里面，只考虑了易感者和感染者，并且感染者不能够恢复，此类病症有 HIV 等，模型如下：
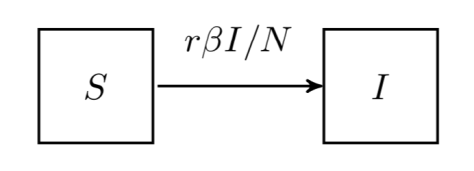
其微分方程就是：
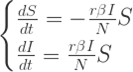
这个微风方程近似解法如下：
通过数值模拟的结果：
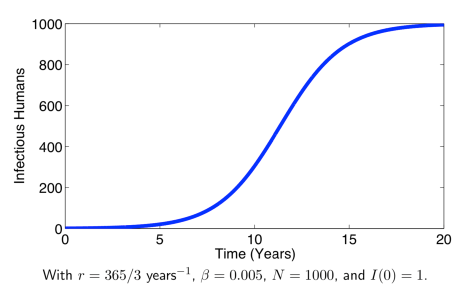
在SI模型的假设下，全部人群到最后都会被感染。
二、SIS模型（Susceptible-Infectious-Susceptible Model）
除了HIV这种比较严重的病之外，还有很多小病可以恢复并且反复感染，例如日常的感冒，发烧等。在这种情况下，感染者就有一定的几率重新转化成易感者。如下图所示：
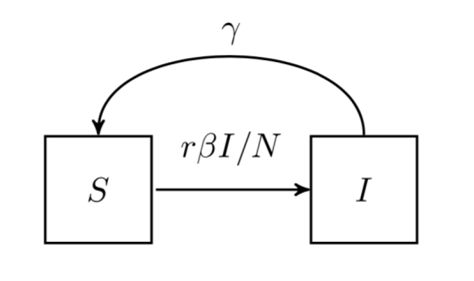
其微分方程是：
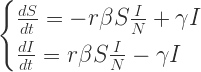
初始值：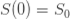
，
。
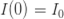这个方程的数值近似解：
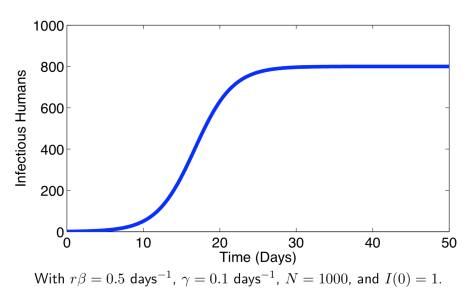
三、SIR 模型（Susceptible-Infectious-Recovered Model）
很多时候，感染者在康复了之后就有抗体，于是后续就不再会获得此类病症，这种时候就需要考虑SIR模型。此类病症有麻疹，腮腺炎，风疹等。我们熟悉的SIR模型是基于疫情流行区域的总人数、感染人数、易感人数、病愈人数和时间之间的如下关系：
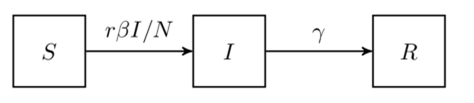
其微分方程是：
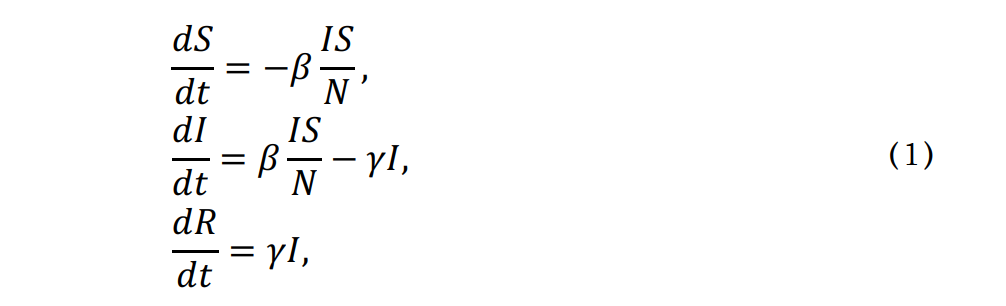
这些方程里的参数和为常数，反映了特定疫情的特征。这些方程貌似简单，但由于常数和是同一数量级，导致方程属于高度耦合的非线性类型，实际上无法求解析解，需要用数值解来提供预测结果。在疫情扩散过程中的早期，由于开始时易感人群也就是总人数，即 ≈ ，我们可以简化感染人数和时间的关系为：
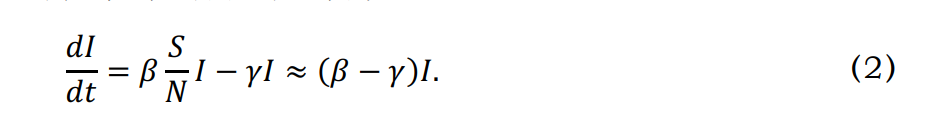
由此可得到感染人数的近似解为：
这一关系表明，近似的感染人数总数是时间的指数函数。这里的常数和应该根据疫情的特点来确定，从而实现感染人数的估计。当然，疫情防控措施也会影响这些参数，反过来也反映了防控措施的效果。这些参数一般是根据流行病学的统计结果得到的，会在疫情的流行过程中得到反映。也就是说，我们也可以根据实际疫情报告来决定这些参数。由于我们已经积累了一些疫情实际数据，基于SIR分析的回溯拟合可以精确地确定这些参数。
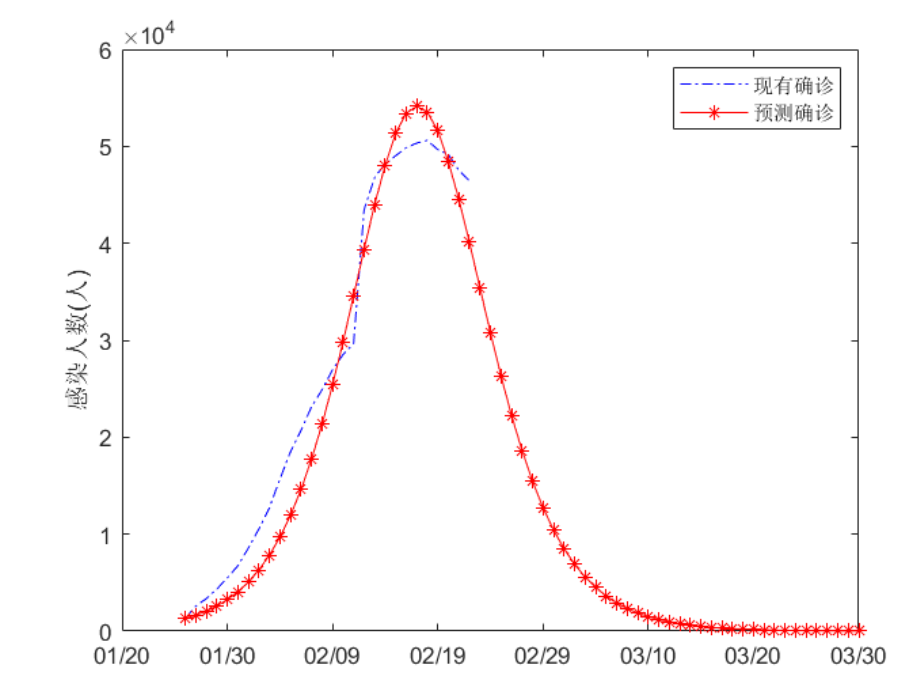
SIR模型的一些近似结果（预测新冠病毒的有症状的确诊病例）：
四、总结
最后，除了以上的 SI，SIS，SIR 模型中，还考虑进去。除此之外，如果把潜伏期、潜伏期的传染情况也加进去考虑，还有SIRS模型，SEIR模型等，但是不管怎么变化都是基于SIR这个微分模型，而且有时候考虑的参数越多不一定越准确，比较本身参数就不是绝对精确。