一、前言
我已经毕业十多年了,大学本科数学四年,前两年我的大部分精力都投入到数学学习,特别是数学分析、高等代数和解析几何,这三门课程我学得非常好,另外运筹学和数学模型学得也还可以,复变函数我自认为理解很好,但是考试分数很差。后两年我开始对编程感兴趣,只有一半多的时间放在专业课上,专业课程包括概率论、实变函数、数值分析、抽象代数、数学物理方程、数论基础、应用数理统计、最优化原理与算法、偏微分方程数值解和泛函分析,这些课程里除了概率论和数理统计,其他的课程学得就没有前两年那么深入。
这段时间重新翻了翻大学的课程,印象最深的还是那三大基础课程:数学分析、高等代数和解析几何,加上概率论和数学模型,我基本都还能捡回来。我感叹大学的自己曾经一只脚迈进现代数学大门,后来抽身离开;现在还想打开这扇门,虽然里面风景独好,但是发现已经迈不进去了。我重新阅读这些图书,一方面是促进自己在算法和建模方面的工作,另一方面是希望对数学史了解更深刻。
二、数学分析
这门学科可以追溯到古希腊欧多克索斯,他提出的穷竭法第一次引出极限理论,另一位伟大的数学家阿基米德则真正让微积分初现萌芽,他是用穷竭法求出了抛物线弓形的面积。由于欧洲罗马帝国和中世纪对古希腊文明的摧残,一直到17世纪文艺复兴之后,微积分才开始得到发展,帕斯卡、费马、沃利斯和巴罗都触及到了微积分的边缘,他们的一些工作其实已经反映出了微积分思想。
真正创立微积分的人是牛顿和莱布尼茨,牛顿为了研究物理发明微积分,他采用的是流数术;莱布尼茨则采用更加数学的方法创立了微积分,他的方法一直保留至今。客观公正的说,他们两位都是分别独立创立了微积分。这时候的微积分是建立在不严密的基础之上,特别是对于无穷量小这个概念非常模糊,虽然如此,但是基于不严密的微积分,欧拉、拉格朗日、拉普拉斯、勒让德和傅立叶深刻发展了微积分,并且获得了大量原创性成果。
微积分严密化工作一直到了19世纪才完成,从波尔查诺、阿贝尔和柯西开始,一直到维尔斯特拉斯、戴德金、黎曼和达布,他们先摆脱了无穷小量的幽魂,建立实数理论,完成极限的严格定义和证明,最终完成现代数学分析体系的建立。大学本科的数学分析也只是讲到了19世纪末。
20世纪的分析学最深刻的变革是勒贝格开创测度论,以此发展出了实变函数,以此衍生了理论化的概率论和随机过程,同时复数的引入,也发展出了基于复变函数的复分析。而以函数空间为基础的泛函和算子理论,则发展出了泛函分析,泛函分析里的希尔伯特空间、巴拿赫空间和广义函数论在物理学获得应用。三角级数发展成傅立叶分析。多变量函数和多维空间的曲面的研究,则发展出了微分几何学、偏微分方程和流形分析。一元线性空间(即线性方程组)理论问题基本都被解决,非线性分析则成为最活跃的数学分析分支之一。这里值得一提的是:罗宾逊将实数推广到超实数,引出了非标准分析。目前,无穷维的微积分理论并没有建立,注意:这里的无穷维并不是指N维空间,因为一般意义上的N维空间并不是无穷维。
现在活跃的纯数学分析研究方向主要是非线性分析和偏微分方程,这个方向可以产生大量的论文,但是很难产出原创性的理论。另外一方向就是无限维微积分的研究,但也仅限于巴拿赫空间的大量研究,更普遍的无限维微积分似乎已经超出人类的智力范围。非纯粹的数学分析主要就是和其他数学学科的混合研究,比如调和分析。
三、高等代数
代数是数学史上最古老的一门学科之一,甚至可以说曾经的代数就代表数学,从最基础的整数和算术到方程,再到统一的线性代数,直至抽象代数,代数的发展一直伴随着人类文明的历史。人类最开始结绳计数就开始和代数(即算术)打交道,而5000多年之前的两河流域文明就出现算术系统,特别是巴比伦文明已经开始研究代数方程。古埃及人、古希腊人和古代中国从几何角度去探讨过方程求解,毕达哥拉斯则认为“万物皆数”,欧几里德证明素数无限。一直到了古罗马时期,被誉为“代数之父”之一的丢番图正式研究不定方程。
波斯帝国诞生了另外一位也被尊为“代数之父”的花拉子米,他的《代数学》是第一本解决一次方程及一元二次方程的系统著作。中世纪的欧洲,东方数学家在代数方面取得辉煌成就。古波斯的欧玛尔·海亚姆发展出代数几何,并且且找出了三次方程的一般几何解法;古印度的摩诃吠罗和婆什迦罗与古中国的朱世杰解出了许多特定的三次、四次、五次方程的解;古中国的秦九韶甚至证明了中国剩余定理,即关于互素和模的定理。
文艺复兴之后的欧洲开始研究从东方传来的方程求解,逐渐打开代数大门,特别是对高次方程的一般解法的研究,阿贝尔和迦罗华做出突出贡献,阿贝尔证明五次方程的根式解的不可能性并在椭圆函数的研究中提出阿贝尔方程式,英年早逝的迦罗华则发展出了群论。莱布尼茨继续发展了日本数学家关孝和提出的行列式概念,并通过矩阵来解出线性方程组,加布里尔·克拉默则在更一般情景研究矩阵和行列式上。到了埃米诺特,基于迦罗华理论引伸出了更抽象更一般的群、环、域,并提出了抽象代数。
抽象代数是人类智慧的集中体现,它使得“代数”这个词在数学世界的意义,从“方程理论”换变成“代数结构理论”,大量天才数学家对抽象代数进行研究。恩斯特·斯坦尼兹研究过一般的域、大卫·希尔伯特、埃米尔·阿廷与埃米·诺特研究过可交换群与一般的环,恩斯特·库默尔、利奥波德·克罗内克与理察·戴德金研究过可交换环的理想,以及费迪南德·格奥尔格·弗罗贝尼乌斯与伊赛·舒尔研究过群的表示理论。
数论其实也算是代数的一个分支,数论被认为是最纯粹的数学,而数量的核心研究对象是素数,真正让数论成为一们学科是由费马、梅森、欧拉、高斯、勒让德、黎曼、希尔伯特等人发展而来。目前数论的研究围绕几个大的猜想,特别是黎曼猜想,黎曼猜想不仅涵盖了素数分布,还包含了复分析、解析数论等知识。
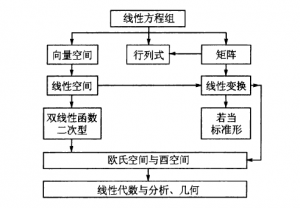
我大学所学的高等代数,由一元线性方程组的研究,先引出了向量空间、矩阵,接着探讨线性空间和线性变换,然后抽象出欧氏空间和酉空间,最后从抽象的角度探讨线性代数、几何和分析三者的关联。下图高度概括这种关系:
四、解析几何
几何的诞生和人类文明同时发展,无论是尼罗河边上的古埃及人、古希腊哲人,还是两河流域的巴比伦人和古代中国人,都对几和进行了或多或少的研究,但是真正数学意义上的几何则来自古希腊人。公元前六世纪泰勒斯的时代,西方世界开始将几何学视为数学的一部分。公元前三世纪,几何学中加入欧几里德的公理,产生的欧几里得几何是往后几个世纪的几何学标准。阿基米德发展了计算面积及体积的方法,许多都用到积分的概念。阿波罗尼奥斯完成圆锥曲线理论,这些工作为一千八百多年后开普勒、牛顿、哈雷等数理天文学家研究行星和彗星轨道提供了数学基础。
欧洲中世纪期间因为对天文学的研究,所以保留了几何知识的学习,但都是掌握在神父手上,并没有取得任何进展。天文学中有关恒星和行星在天球上的相对位置,以及其相对运动的关系,都是后续一千五百年中探讨的主题。几何和天文都列在西方博雅教育中的四术中,是中古世纪西方大学教授的内容之一。
勒内·笛卡儿发明的坐标系以及当时代数的发展让几何学进入新的阶段,像平面曲线等几何图形可以由函数或是方程等解析的方式表示。这对于十七世纪微积分的引入有重要的影响。透视投影的理论让人们知道,几何学不只是物体的度量属性而已,透视投影后来衍生出射影几何。欧拉及高斯开始有关几何物件本体性质的研究,使几何的主题继续扩充,最后产生了拓扑学及微分几何。现代概念上的几何其抽象程度和一般化程度大幅提高,并与分析、抽象代数和拓扑学紧密结合。
这里重点提出非欧几何(或者叫罗巴切夫斯基几何),这是人类颠覆传统欧几里德几何观念的一次巨大思维飞跃,也是几何学发展的新里程碑。非欧几何曾经在高斯的脑子里酝酿,但他没有深入研究,最终是波约尔和罗巴切夫斯基创立,而因为罗巴切夫斯基的方式更完美,做的工作也更多,所以也叫罗巴切夫斯基几何。非欧几何后续又由黎曼、庞加莱等数学家发展和改进,并且需求数学逻辑上的理论支持,最终在20世纪初被爱因斯坦运用于广义相对论,非欧几何的应用于广义相对论与微积分应用于经典物理学一样值得称颂。
解析几何是欧几里德几何的现代版本,20世纪下半叶中有大幅的进展,主要是因为让-皮埃尔·塞尔及亚历山大·格罗森迪克的贡献,这也产生了概形以及代数拓扑学一些方法的重视,包括许多的上同调理论。千禧年大奖难题中的霍奇猜想就是解析几何学的问题。
低维度代数簇、代数曲线及代数曲面的研究以及三维代数簇(algebraic threefolds)的研究都有很多进展。Gröbner基理论及实代数几何应用在现在解析几何的一些子领域中。算术几何(Arithmetic geometry)是结合了解析几何及数论的一个新的领域。另外一个研究方向是模空间及复几何。代数几何的方法广泛的用在弦理论及膜宇宙理论中。
我所学习的解析几何主要是先从向量代数出发,建立仿射坐标系,并研究空间的直线、平面和曲面,同时学习仿射坐标变换、二次曲面的仿射理论,放射变化和保距变换。最后还学习了射影几何的基本知识。